Y'aurait à voir du côté du calcul des tiers exacts (33,33333% et 66,66666%), mais pas toujours et pas dans tous les cas :
alert(570.67*100); donne 57066.9999999999
alert(100.67*100); donne 10067
alert(570.33*100); donne 57033.0000000001
alert(570.34*100); donne 57034
alert(100.33*100); donne 10033
Là où ça se complique franchement, c'est que :
alert(510.67*100); donne 51067
alert(520.67*100); donne 52066.9999999999
alert(420.67*100); donne 42067
Alors on se dit qu'on va tester les valeurs entre 510 et 520 :
alert(511.67*100); donne 51167
alert(512.67*100); donne 51266.9999999999
Bref, y' a sûrement une règle, mais laquelle ? Aux matheux de répondre...
Pas mal non plus :
alert(600.67*100); donne 60066.9999999999
alert(700.67*100); donne 70067
Du coup j'ai cherché la limite entre 600 et 700 :
alert(654.67*100); donne 65466.9999999999
alert(655.67*100); donne 65567
Modifié par Arsene (15 May 2008 - 09:49)
alert(570.67*100); donne 57066.9999999999
alert(100.67*100); donne 10067
alert(570.33*100); donne 57033.0000000001
alert(570.34*100); donne 57034
alert(100.33*100); donne 10033
Là où ça se complique franchement, c'est que :
alert(510.67*100); donne 51067
alert(520.67*100); donne 52066.9999999999
alert(420.67*100); donne 42067
Alors on se dit qu'on va tester les valeurs entre 510 et 520 :
alert(511.67*100); donne 51167
alert(512.67*100); donne 51266.9999999999
Bref, y' a sûrement une règle, mais laquelle ? Aux matheux de répondre...
Pas mal non plus :
alert(600.67*100); donne 60066.9999999999
alert(700.67*100); donne 70067
Du coup j'ai cherché la limite entre 600 et 700 :
alert(654.67*100); donne 65466.9999999999
alert(655.67*100); donne 65567
Modifié par Arsene (15 May 2008 - 09:49)


Parce que si tu teste =>
alert((570.67*1000)/10)
héhé
a écrit :
Bref, y' a sûrement une règle, mais laquelle ? Aux matheux de répondre...
Pas mal non plus :
alert(600.67*100); donne 60066.9999999999
Une règle ? Depuis quand une multiplication d'un chiffre à deux décimales par 100 donne un chiffre à virgule ??? O_o
mais test mon code du dessus tu va te pendre

Oui je sais vous aimez quand je viens poster ici

Modifié par ffwrude (15 May 2008 - 13:37)
ffwrude a écrit :
Une règle ? Depuis quand une multiplication d'un chiffre à deux décimal par 100 donne un chiffre à virgule ??? O_o
Depuis que les ordinateurs stockent les nombres réels dans un format à virgule flottante, format efficace en termes de stockage et permettant des calculs très rapides, mais qui a un inconvénient pour les calculs mathématiques: certains nombres réels ne peuvent pas être exprimés dans ce format. C'est le cas notamment de pi, et peut-être celui de 570.67 et 570.33 (exprimés avec 5 chiffres en base 10, mais peut-être pas exprimables en 24 chiffres en base 2).
Hop:
http://en.wikipedia.org/wiki/Floating_point
http://en.wikipedia.org/wiki/Floating_point#Accuracy_problems
Modifié par Florent V. (15 May 2008 - 13:26)
Ce que tu me dis c'est qu'en réalité 570.67 est sous la forme 576.6700000000000003 des sa "mise en place" ? Je comprend pour une division ce genre de chose comme pour un calcul de type 3x1 /3 qui ne donne pas forcement 1. Mais le je ne comprend pas comment 576.67*100 ne donne pas 576670 mais 576670,0000000000003.
Peut tu éclaircir ? Car dans les articles données il y'à bien un "chapitre" sur la multiplication mais je ne comprend pas bien.
Rude
Modifié par ffwrude (15 May 2008 - 13:37)
Peut tu éclaircir ? Car dans les articles données il y'à bien un "chapitre" sur la multiplication mais je ne comprend pas bien.
Rude
Modifié par ffwrude (15 May 2008 - 13:37)
ffwrude a écrit :
Parce que si tu teste =>
alert((570.67*1000)/10)
héhé
En fait, ce n'est pas le calcul qui est mauvais, mais l'affichage du résultat, l'interpréteur ayant le choix entre afficher 57067 et 57066.99999999... (on va faire preuve d'imagination, pour le reste du post les "..." ca veut dire "ca continue jusqu'à l'infini") et visiblement il fait le mauvais choix, du moins pas celui qu'on attend, mais le résultat binaire de l'opération avec les virgules flottantes est lui le même entre ((570.67*1000)/10) et (570.67*100) mais le fait d'avoir ecrit l'opération autrement fait que l'interpréteur va transformer le résultat binaire autrement. Il y a surement une règle au niveau de celui-ci qui le fait choisir (ou alors un Math.random()
 )...
)...Il me semble qu'en mathématiques il est admis que 0.99999999999... est strictement égal à 1. Preuve en est (1/3) = 0.333333333333333...., donc
3*(1/3) = (3/3) = 1
3*(1/3) = 3*0.33333333333.... = 0.999999999999...
donc 0.99999999999... = 1

Edit : Et pour résoudre ce problème, il vaut mieux décider soit même de la précision des résultats des données que l'on veut traiter et faire des arrondis...
Edit 2 : Ce que j'ai écrit en italique est faux
 , alert((570.67*1000)/10==(570.67*100)) renvoyant un joli "false"... désolé et désolé aussi à mes anciens professeurs qui il y a quelques années nous faisait faire à la main des calculs avec des virgules flottantes. Avec du recul je pense pouvoir dire que 99.99999999999...% des étudiants ont oublié comment on fait, dommage j'aurai pu faire le malin aujourd'hui...
, alert((570.67*1000)/10==(570.67*100)) renvoyant un joli "false"... désolé et désolé aussi à mes anciens professeurs qui il y a quelques années nous faisait faire à la main des calculs avec des virgules flottantes. Avec du recul je pense pouvoir dire que 99.99999999999...% des étudiants ont oublié comment on fait, dommage j'aurai pu faire le malin aujourd'hui...
Modifié par skywalk3r (15 May 2008 - 14:01)
a écrit :
3*(1/3) = (3/3) = 1
3*(1/3) = 3*0.33333333333.... = 0.999999999999...
donc 0.99999999999... = 1
C'est un exellent exemple.
Mais comme dit plus haut, dès qu'il y'à de la division je comprend. C'est l'étape de la multiplication que je ne comprend pas. Il n'y à PAS de virgules flotantes dans le résultat de l'opération 570.67*100 (ou alors c'est que j'ai raté quelque chose... ce qui est certain vu que je n'ai toujours pas compris vos réponses).
Rude
skywalk3r a écrit :
Il me semble qu'en mathématiques il est admis que 0.99999999999... est strictement égal à 1.
Non.
skywalk3r a écrit :
Preuve en est (1/3) = 0.333333333333333....
Cette égalité est fausse. 1/3 est égal à 2/6 ou 3/9 si tu veux, mais certainement pas à 0.333333333333333... quel que soit le nombre de 3 après la virgule. Tu peux en mettre un milliard que l'égalité ne serait pas juste.
ffwrude a écrit :
Il n'y à PAS de virgules flotantes dans le résultat de l'opération 570.67*100 (ou alors c'est que j'ai raté quelque chose... ce qui est certain vu que je n'ai toujours pas compris vos réponses).
Pour réaliser l'opération, le langage doit stocker le nombre 570.67 et le nombre 100 en mémoire. Pour cela il doit choisir un format binaire, à priori un nombre à virgule flottante codé sur N bits (8, 16, 24, 32... je ne sais pas exactement... je crois que c'est 24 mais je dis peut-être une bêtise). Si 570.67 n'est pas exprimable de manière juste sur ce nombre de bits (de même que 1/3 ou pi ne sont pas exprimables de manière juste même avec un milliard de décimales!), alors ce n'est pas 570.67 qui est stocké mais un nombre s'en approchant.
Après, je suppose que les différents langages ont des mécanismes plus ou moins complexes pour éviter ce genre de problèmes. Je suppose que ce n'est pas pour rien qu'il existe des langages de programmation très utilisés en recherche mathématique et généralement pour toutes les applications scientifiques...
Pour les détails, désolé mais je n'en sais pas plus (je dis peut-être des bêtises d'ailleurs). Et j'avoue ne pas avoir tout compris (et ne pas avoir tout lu
 ) de l'article que je cite comme référence. C'est que je suis littéraire de formation, moi.
) de l'article que je cite comme référence. C'est que je suis littéraire de formation, moi. 
Modifié par Florent V. (15 May 2008 - 14:14)
Florent V. a écrit :
Non.
En fait, oui, en cherchant un peu sur Google, il y a plein de façon de le montrer et de montrer que si l'on accepte pas ce principe la plupart des lois mathématiques s'effondrent...
Florent V. a écrit :
Cette égalité est fausse. 1/3 est égal à 2/6 ou 3/9 si tu veux, mais certainement pas à 0.333333333333333... quel que soit le nombre de 3 après la virgule. Tu peux en mettre un milliard que l'égalité ne serait pas juste.
Mais un milliard est bien plus petit que l'infini... c'est bien là le soucis. L'infini n'existe pas vraiment mais s'il n'existe pas, les chiffres n'ont plus de sens. Il y a un principe mathématique qui dit que deux nombres x et y sont égaux s'il n'existe pas de nombre a tel que x<a<y, si x est égal à 0.999999... que l'on peut noter sous forme d'une suite sommée comme ceci :
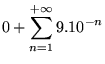
et y égal à 1, il n'existe pas de a vérifiant x<a<y donc x=y.
a écrit :
(de même que 1/3 ou pi ne sont pas exprimables de manière juste même avec un milliard de décimales!)
Attention, l'infini est un concept est non une valeur proche de un milliard... (c'est un formule rhétorique je te rassure je suis pas en train de te prendre de haut, je ne me le permettrait pas) Cela dit, informatiquement parlant on peut stocker 1/3 de manière exacte (sous forme d'un rationnel c'est à dire "1/3") alors que pi est un irrationel, il n'existe pas de moyen de le stocker de manière exacte (seulement des approximations qui sont vraies jusqu'à un certain nombre de décimales)...
Enfin bref, je n'aurais pas aimé être le type qui a du réfléchir à tout ça pour le mettre sous forme de 1 et de 0...
Et encore une fois Florent.V ... encore une fois... c'est grace à toi que je comprend.... Avoue ! tu n'es pas de cette planète pour savoir autant ! lol
En tout cas j'aime beaucoup la discussion lancée même si je peux pas tout suivre ... Je ne sais même pas quelle est la lettre étrange (un sigma ?) que tu as mise skywalker....
Mais pourquoi ne serait t'il pas stockable ? Qu'est-ce qui déclenche cette instockabilité ?
Modifié par ffwrude (15 May 2008 - 17:39)
En tout cas j'aime beaucoup la discussion lancée même si je peux pas tout suivre ... Je ne sais même pas quelle est la lettre étrange (un sigma ?) que tu as mise skywalker....
a écrit :
Si 570.67 n'est pas exprimable de manière juste sur ce nombre de bits
Mais pourquoi ne serait t'il pas stockable ? Qu'est-ce qui déclenche cette instockabilité ?
Modifié par ffwrude (15 May 2008 - 17:39)
skywalk3r a écrit :
Il y a un principe mathématique qui dit que deux nombres x et y sont égaux s'il n'existe pas de nombre a tel que x<a<y, si x est égal à 0.999999... que l'on peut noter sous forme d'une suite sommée comme ceci :
upload/13941-img1.png
et y égal à 1, il n'existe pas de a vérifiant x<a<y donc x=y.
Ok pour ça. J'ai lu la phrase «Il me semble qu'en mathématiques il est admis que 0.99999999999... est strictement égal à 1» de manière littérale et sans penser au concept d'infini.

Je voulais juste qu'il soit claire que toute notation de 0.999999... avec un nombre fini de décimales n'était pas égal à 1, histoire que les lecteurs n'aillent pas croire que si Javascript affiche des 0.999999999999... quand il devrait afficher des 1 c'est à cause d'un principe mathématique qui rendrait l'affirmation pi = 3,1415926536 exacte.
Il me semble que la démonstration que tu évoques n'est pas liée au problème de la justesse des calculs avec des nombres stockés sous forme de nombres binaires à virgule flottante.
(Pour compléter l'explication de yahrou, et en termes plus profanes: la formule toute bizarre donnée par skywalk3r fait la somme de 0,9 + 0,09 + 0,009 + 0,0009 + 0,00009... et ainsi de suite jusqu'à une infinité de zéro avant le 9. Donc on obtient 0,999999... avec une infinité de 9 après la virgule.)
ffwrude a écrit :
Mais pourquoi ne serait t'il pas stockable ? Qu'est-ce qui déclenche cette instockabilité ?
Si j'ai bien compris, un format à virgule flottante comprend un nombre de bits limité pour la valeur «brute», et un marqueur qui indique à quel endroit doit être placée la virgule. Un peu comme si on écrivait 02000000057067, où les deux premiers chiffres forment un nombre qui indique le placement de la virgule à partir de la fin, et les douze chiffres suivants stockent la valeur «brute», sans virgule. On peut même imaginer que le marqueur sur deux chiffres correspond à un nombre positif s'il est inférieur à 51, et à un nombre négatif s'il est supérieur ou égal à 51 (51 serait -1, 52 serait -2, 74 serait -24, etc.). Ce qui nous permet d'exprimer 57067*10^N, ou N est un entier compris entre -50 et 49 (si je me suis pas planté dans ma propre supposition).
Bon. 57067 en binaire c'est 1101111011101011. Mais 570,67 c'est 1000111010,<quelquechose>, où le <quelquechose> est l'équivalent binaire (base 2) de 0,67 (base 10). (Pour information, je n'ai pas trouvé de moyen simple de calculer ce <quelquechose>, mais c'est possible avec la bonne méthode.) Maintenant, mettons qu'on stocke notre nombre sur 24 bits. La partie entière (570) occupe déjà 16 bits. Il nous en reste donc 8. Si la partie décimale (.67) ne correspond à aucun nombre binaire de moins de 9 bits, eh bien on est dans la merde: il faudra arrondir. Et un nombre arrondi n'est pas exact (et donc son utilisation dans un calcul fait que le résultat sera faux).
Bien sûr, si on stocke nos nombres à virgule flottante sur 128 bits (16 octets), le risque de devoir arrondir notre nombre est moins grand.
Voilà pour ce que j'ai compris pour ma part. Je rappelle encore que je suis mal informé sur le sujet, pas très doué en maths, et donc je raconte peut-être des bêtises.

Oups, peut-être ai-je oublié de que je parlais de principes purement mathématiques qui ne s'appliquent pas, comme Florent V. l'a précisé à, l'informatique.
Je me rappelle que dans un de mes cours d'info à l'IUT un prof nous avait expliqué et il nous demandais de convertir des nombres avec décimales en base 10, en binaire à virgule flottante... bah il fallait bien un A4 de brouillon pour obtenir un résultat qui était faux une fois sur deux
J'ai essayé de retrouver aujourd'hui mais j'y suis toujours imperméable... si quelqu'un pije le truc ce serait bien de nous l'expliquer
Modifié par skywalk3r (15 May 2008 - 22:01)
Je me rappelle que dans un de mes cours d'info à l'IUT un prof nous avait expliqué et il nous demandais de convertir des nombres avec décimales en base 10, en binaire à virgule flottante... bah il fallait bien un A4 de brouillon pour obtenir un résultat qui était faux une fois sur deux

J'ai essayé de retrouver aujourd'hui mais j'y suis toujours imperméable... si quelqu'un pije le truc ce serait bien de nous l'expliquer

Modifié par skywalk3r (15 May 2008 - 22:01)
Juste pour info, javascript stocke tous les nombres, qu'ils soient à virgule flottante ou non, selon le format float, qui est sur 32 bits.
Dans un nombre à virgule flottante écrit en binaire, on a 3 parties :
- Le bit de signe
- La valeur réelle
- L'exposant qui possède lui aussi son bit de signe.
Un nombre s'exprime toujours selon la forme n * 10^m ou n * 2^m (j'ai un doute tout d'un coup). Faudrait regarder la norme IEE754 mais je n'ai pas le temps de vérifier maintenant.
Dans un nombre à virgule flottante écrit en binaire, on a 3 parties :
- Le bit de signe
- La valeur réelle
- L'exposant qui possède lui aussi son bit de signe.
Un nombre s'exprime toujours selon la forme n * 10^m ou n * 2^m (j'ai un doute tout d'un coup). Faudrait regarder la norme IEE754 mais je n'ai pas le temps de vérifier maintenant.

