Bonjour,
"Niuxe" mon projet consiste à partir du contour d'un terrain quelconque de calculer le trajet d'une tondeuse . La tondeuse commence a tondre en suivant le périmètre puis de réduire le périmètre extérieur du passage de la tondeuse pour obtenir un nouveau tracé. La troisième dimension du tableau représente le nombre de passage et contient les segments parallèles à ceux d'origines .
A partir d'un certain nombre de tours, il y a des segments qui se croisent, donc la c'est trop compliqué pour ma petite tête.
"Mathieuu" effectivement le tableau ptspara est une variable globale, je ne pense pas que cela pose problème.
En réalisant votre suggestion , je perds la dimension de mon tableau .
Le tableau ptspara contient les points correspondant au périmètre du terrain , j correspond au nombre de passage de la tondeuse et "long_tab" au nombre de point constituant le périmètre d'origine.
Le problème est qu'en réduisant le périmètre ,le nombre de point peut aussi se réduire .
Je ne connais "très peu" javascript, mais cela me permet de réaliser des dessins . V
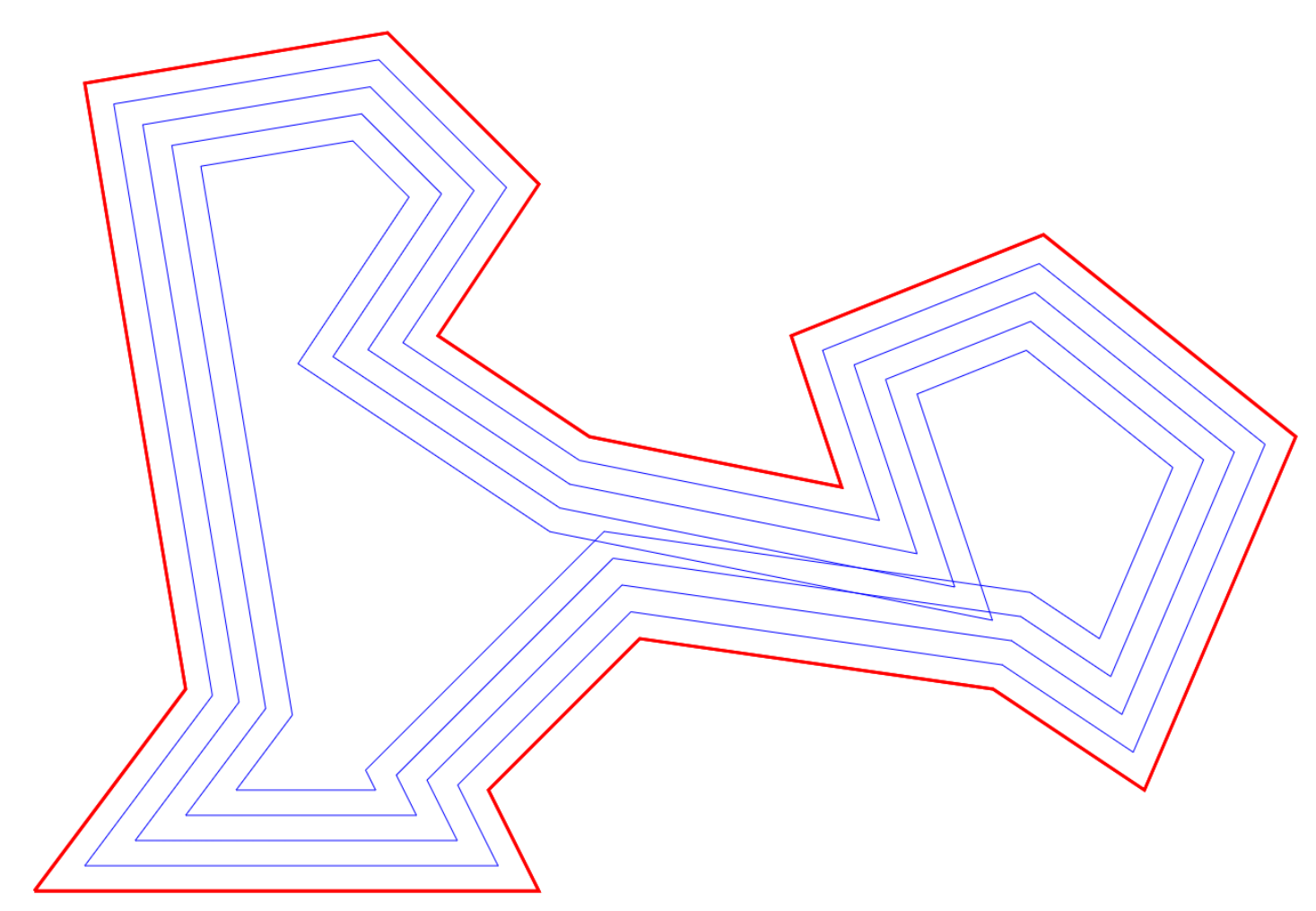
oici le code qui certainement contient des "aberrations", c'est avec plaisir que j'accepterai vos remarques .
<!doctype html> <!-- indique le type de document au navigateur -->
<html lang="fr"> <!-- indique la langue du document -->
<head> <!-- balise ,contient les informations (metadonnées) du document -->
<meta charset="UTF-8" /> <!-- détermine le jeu de caratères , comme la prise en charge des accents-->
<title>calul trajet robot </title> <!-- détermine le texte dans l'onglet du navigateur web -->
</head>
<body> <!-- balise ,détermine le corps du document -->
En info_test
<canvas id="test" width="2000" height="1000"></canvas> <!-- Détermine une surface de dessin en bitmap -->
<script type="application/javascript"> // traitement des données , importation d'un script externe : <script src="javascript.js">
var mespoints = [
[1,1],
[4,5],
[2,17],
[8,18],
[11,15],
[9,12],
[12,10],
[17,9],
[16,12],
[21,14],
[26,10],
[23,3],
[20,5],
[13,6],
[10,3],
[11,1],
[1,1]
];
var coef_droite=[]; // tableau contenant les coefs a,b,bb, et distance entre b et bb y=ax+b et parallele : y=ax+bb
var ptspara=[]; // tableau a 2 dimensions, 1 dimension : numero du point 2ieme dimension= x ou y du point
var tableau_pts=[]; // tableau a 3 dimensions, 1 dimension = nbre de passage ; numero du point 2ieme dimension= dimension : numero du point 3ieme dim:x ou y du point
var long_tab;
var larg_passage =0.5;
long_tab= mespoints.length; // donne la longeur du tableau
function draw() // déclaration de la fonction draw -->
{
const info_test = document.getElementById("test"); // récupére les informations de l'id "test" -->
if (info_test.getContext) { // test l'existance de l'objet contexte de dessin -->
const ctx = info_test.getContext("2d"); // création de la variable pour dessiner -->
ctx.lineWidth=3; // épaisseur du trait
ctx.beginPath();
ctx.font = "48px serif"; // taille des lettres
for (var i =0; i < long_tab; i++)
{
ctx.lineTo(mespoints[i][0]*50,1000-(mespoints[i][1])*50 );
ctx.fillText(i, mespoints[i][0]*50,1000-(mespoints[i][1])*50 ); // ecrit le numero des points du dessin
}
ctx.strokeStyle = "red";
ctx.stroke();
ctx.lineWidth=1; // épaisseur du trait
ctx.beginPath();
for ( j=1; j <3; j++) // affiche les tours de terrain
{
ctx.moveTo (tableau_pts[j][0][0]*50,1000-(tableau_pts[j][0][1])*50);
for (var i =1; i < 16; i++)
{
ctx.lineTo(tableau_pts[j][i][0]*50,1000-(tableau_pts[j][i][1])*50 );
}
ctx.lineTo(tableau_pts[j][0][0]*50,1000-(tableau_pts[j][0][1])*50 );
ctx.strokeStyle = "blue";
}
ctx.stroke();
}
}
function parallele(numero) // calcul les prametres des droites passant par les segments
{
let a,b,dist;
a=(mespoints[numero+1][1]-(mespoints[numero][1]))/(mespoints[(numero+1)][0]-mespoints[numero][0]) ; // calcul de a de y=ax+b
b= mespoints[numero][1]-a*mespoints[numero][0] ; // calcul de b de y=ax+b
if((mespoints[numero+1][0]-(mespoints[numero][0])) >0 ) // Si delta x>0 on soustrait le deplacement
dist=-larg_passage*Math.sqrt(1+a*a) ; //calcul de la distance entre les paralleles de y=ax+b vers y=ax+bb
else
dist=+larg_passage*Math.sqrt(1+a*a) ;
coef_droite.push([a,b,dist]);
}
function calcul_points(nb_passage) // calcul des nouveaux points intersection des droites paralleles
{
for (var k =0; k <(long_tab-2); k++)
{
var xpara,ypara;
var bb12,bb23;
bb12=coef_droite[k][1]+(coef_droite[k][2]*(nb_passage)); // calcul du nouveau coef b de la parallele
bb23=coef_droite[k+1][1]+(coef_droite[k+1][2]*(nb_passage));
xpara=(bb23-bb12)/(coef_droite[k][0]-coef_droite[k+1][0]) ; // calcul de x intersection des droites paralleles x= (bb23-bb12)/(a12-a23)
ypara=(coef_droite[k][0]*xpara + bb12 ); // bb=b+nbr_passage*dist_para
ptspara.push([xpara,ypara]) ;
}
// calcul du dernier point
bb12=coef_droite[k][1]+(coef_droite[k][2]*(nb_passage));
bb23=coef_droite[0][1]+(coef_droite[0][2]*(nb_passage));
xpara=(bb23-bb12)/(coef_droite[k][0]-coef_droite[0][0]) ; // calcul de x intersection des droites paralleles x= (bb23-bb12)/(a12-a23)
ypara=(coef_droite[k][0]*xpara + bb12 );
ptspara.push([xpara,ypara]) ; // sauvegarde des coordonnees dans le tableau
}
for (var j=0; j < (long_tab-1); j++) // il y a 17 points donc 16 droites , calcul des coefficients des droites
{
parallele(j);
document.write('a = '+coef_droite[j][0]+'b = '+coef_droite[j][1]+'distance parallele = '+coef_droite[j][2]+ '<BR>') ;
}
for ( j=0; j < 20; j++) // nombre de passage
{
calcul_points(j);
tableau_pts[j]=ptspara;
ptspara=[];
}
draw(); // appel de la fonction draw -->
</script>
</body>
</html>
Modifié par herve_37 (25 Mar 2025 - 19:22)
)
". Je confirme que ton tableau ptspara n'a pas d'utilité à être globale vu que tu passe ton temps à le réinitialiser. 