18114 sujets
yassinbean a écrit :
Rebonjour,
J'aimerais savoir quel sont les outils les plus fiables pour créer des illustrations pédagogiques (sciences et ingénierie).
MERCI D'AVANCE
Je pense inévitablement, d'abord, au talent du bon illustrateur et à une communauté qui l'aura mandaté.
C'est un peu comme nos doux et ardents ancêtres de la Grotte de Lascaux et d'autres du Portugal, d'Espagne, du Rift africain, de Chine : croyez-vous que le tison de charbon de bois fut l'objet d'un large débat ?
Assurément l'outil ne fera jamais l'Homme. Et qu'à défaut d'outil disponible et si vous avez du talent, vous créerez d'abord vos propres outils, ou encore vous vous accommoderez d'un égal tison de bois charbonné.
Or, ce qui sera toujours percutant/crédible sur le web : des dessins-papier ! ô merveilleux paradoxes ... du tire-ligne à l'encre de Chine, du crayon Comté, du pinceau d'aquarelle, du compas qui fait surtout un trou au milieu du cercle, de la gomme qui arrache la fibre du papier.
Mais mais mais il y a SketchUp Pro / 3D / 2015 avec ses options d'ingéniérie, pas gratuit donc payant (590$) : http://www.sketchup.com/fr/products/sketchup-pro
Je ne peux vous parler de la version Pro. Je ne la connais pas. J'ose croire qu'elle est formidable, grâce à ces animations, ces rendus , ...
Je vous parlerai de la version gratuite. J'aime utiliser (depuis longtemps) SketchUp dans ses versions gratuites (donc rudimentaire en qualité de rendu c-à-d anticrénalage, texture, ombre et lumière).
Je suis devenu "maître" de concevoir des escaliers (escaliers "droits" ou ceux à révolution cylindrique c-à-d hélicoïdaux) car une erreur "colossale" commise que puisse commettre un artisan maçon est de ne pas considérer le développement d'une marche ultime, ou celui de "la marche zéro" (dans le moins pire des cas, car un ami s'en est brisé le cou, dans la nuit obscure, sur son escalier tout neuf ...).
Essayez avec des morceaux de sucre sur la table de votre cuisine : mesurez le développement horizontal pour telle hauteur d'élévation obtenue (de nez à nez : c-à-d de butoir de pied en butoir de pied) ... hi hi hi ! et comparez avec ce que vous aviez présumé.
 Constatez de façon annexe toute hauteur sous-marche (des fois que vous y plantiez votre crâne en passant dessous).
Constatez de façon annexe toute hauteur sous-marche (des fois que vous y plantiez votre crâne en passant dessous).Ici j'aime vous relater une visite. A Chinon où tout est construit de pierre de tuffeau que Rabelais adorait pour sa couleur de lait non écrémé taillable (non le beurre) à l'outil mou, un escalier à révolution cylindrique présentait de palier en palier des portails de faibles hauteurs : mais pourquoi cet autoclave de moinesses était-il si bas ? Personne n'eût pu avancer une explication.
J'osai ceci : -"Pour leur interdire de porter des hauts talons."
Madame la Propriétaire, absolument laïque, ne me répondit point tout de suite. Mais toutefois et selon son autorité, je compris qu'elle avait compris, et qu'elle envisageait de rapprocher notre entendement.
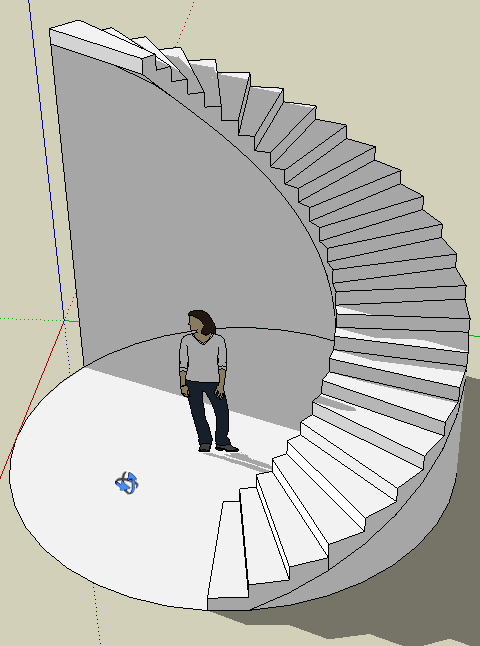
Une astuce toute simple mais géniale : partez du produit fini (je ne parle plus de l'antique propriétaire laïque) tel que vous osez l'imaginer (qui, dans votre tête est LA chose idéale ! oubliez la propriétaire), et voyez si votre bon délire parvient à s'intégrer aux relevés réels ; produit fini que, couche par couche vous éplucherez pour véritablement le construire, le dé-construire, le re-construire.
Sachez qu'un authentique expert en construction (ingénieur et architecte) (par exemple Expert près les Tribunaux) vous retournera : -"Un escalier, Monsieur, ce n'est jamais facile !"
Vous procéderez (peut-être et par votre génie créateur) comme François Ie Premier et Leonardo da Vinci pour édifier Chambord : construire un Château autour d'un escalier plutôt monumental à double révolution intégrée : un premier escalier gravit et dessert les étages pair, un second escalier intégré au premier dessert uniquement les étages impair (ou par des paliers séparés), hors que des personnes qui fréquentent simultanément les deux escaliers, mais en descente et montée ! ne se croisent jamais ...
Essayez de conceptualiser, de visualiser, et d'illustrer : SketchUp sera votre ami si vous saviez y faire ...
Voici une proposition Chambordienne :
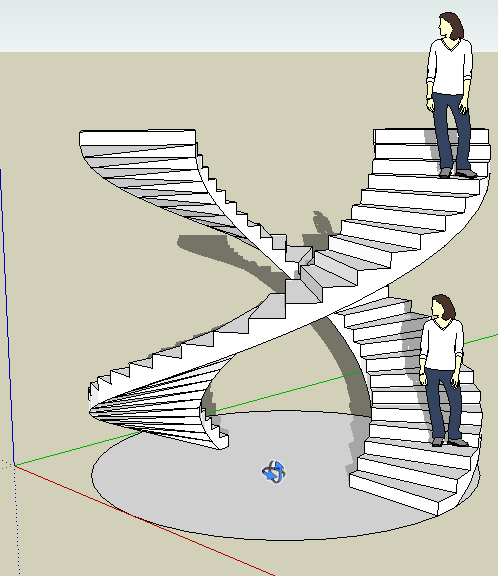
Il suffira que vos maçons édifient un cylindre au coeur des 2 volées d'escalier : vous obtiendrez deux flux distincts de déplacement de personnes, lesquelles seront totalement indépendantes et invisibles les unes des autres. Ces deux escaliers seront parfaitement praticables, sans contraintes de hauteur sous "plafond", ou autre hauteur de marche, de profondeur notamment ...
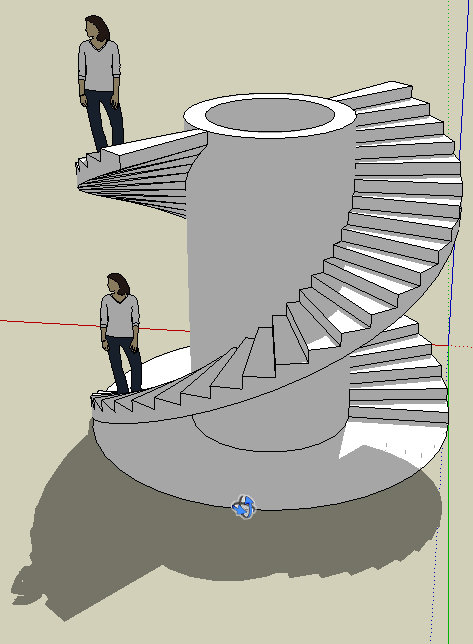
Amusant, non ? C'est un peu comme ça que l'on dessine aujourd'hui les sous-marins nucléaires, les Rafales et autres Airbus ! Même qu'un Roger de synthèse (et de petite taille) est censé accéder au moindre recoin pour intervenir, démonter et réparer ...
Une dernière astuce pour l'escalier hélicoïdal : prenez une feuille papier A4, et tracez-y au stylo une diagonale bien droite c-à-d rectiligne (au besoin prenez une latte, une règle de dessinateur) ; joignez ensuite, à l'aide de vos seuls 10 doigts (de la main car avec les pieds ...) 2 des bords opposés afin d'obtenir un cylindre. Youpie ! Eurêka ! Miracle ! Putain de merde ! vous avez trouvé la vraie 3D de la course de votre futur escalier. Stupéfiant, non ?
Ainsi, sur le chantier de votre nouvelle maison, le maçon se contentera de courber quelques fines feuilles de contreplaqués où vous auriez dessiné chacune de vos marches ...
En soi, pour satisfaire le sujet du topic : oui SketchUp est en cela fiable qui illustre sans faillir une prospection, une projection mentale en 2D (plan : dessus dessous / élévation : face derrière gauche droite) et 3D (...).
Note : quoi que SketchUp ne puisse dessiner que le cercle et non l'ellipse, vous y obtiendrez l'ellipse en considérant que ellipse et cercle sont jumeaux : dénaturer par son échelle la coordonnée X ou Y d'un cercle, et vous obtenez une ellipse ... Bon ! je pourrais vous dessiner cercle et ellipse sur le sol de votre jardin : deux bouts de bois plantés, une cordelette longue du diamètre d'un cercle, nouée de part et d'autre aux bouts de bois ; faites courir le long de la corde et sur le sol un traceur ; modifiez l'écartement de façon répétée en déplaçant un bout de bois, jusqu'à le joindre à l'autre, vous aurez tracé 50 ellipses qui deviennent enfin un cercle parfait. Si l'illustrer était nécessaire, c'est certain SkectchUp ferait votre affaire ... Ah ! cercle et ellipse ont 5000 ans d'histoire plutôt bâtarde (l'ellipse n'a pu être calculée que depuis 150 ans ; et sa formule mathématique s'applique pile-poil au cercle, comme s'il avait suffit d'y penser).
Pour le fun avec SketchUp : en entrant des mesures au clavier (numérique) plutôt que d'une façon intuitive (à la souris ou au pavé), vous pourriez très facilement construire depuis un cube une sphère "architecturale moderne" sur un dodécaèdre élémentaire façonné de pentagones et d'hexagones assemblés puis redivisé en triangles depuis le centre de la sphère retrouvé ... A toute bonne fin d'obtenir une structure auto-portante et indéformable ! Ouais ouais. C'est la géode : http://rouxjeanbernard.ch/AM/html/amch104.html
Bon ! Là c'est vraiment l'extase quand on fait pivoter le bon résultat en 3D ... avec un éclairage de printemps (grâce à son ombre).
Question : pour une surface donnée (aux parois souples mais non-extensibles), par quelle apparence peut ou doit avoir son volume maximal ?
Réponse : la sphère, et rien que la sphère. Les exemples quotidiens sont nombreux, des bulles de votre shampoing de votre douche du matin, aux bulles de votre verre de champagne du soir. La question eût pu être rédigée inversement : pour un volume maximal, quelle est la figure tridimensionnelle requise pour la surface de son enveloppe ? La sphère ; non le cube, non le prisme , non ... autre chose que la sphère.
D'aussi loin que notre cerveau puisse venir (du poisson reptilien), nous demeurons fascinés par la sphère. Empreinte mémorielle génétique reloaded par le ventre de notre mère où, pour la plupart d'entre nous, nous avons d'abord prospéré.
Fascinant, non ? Comme si le propre de l'Homme, c'était (et ça reste) la superstition et une croyance obscure.
Là SketchUp ne vous aidera qu'à moitié. Il calculera bien votre surface (plane ou sphérique), mais retournera maladroitement un volume quelconque ... (peut-être un bug récurrent et superstitieux).
Autres créations et illustrations avec SketchUp :
Modifié par senteur_honrable (05 Feb 2015 - 10:35)
Bonjour,
"J'aimerais savoir quel sont les outils les plus fiables pour créer des illustrations pédagogiques (sciences et ingénierie)."
Ta question est trop vague, en tout cas pour moi : images 2D, images 3D, vectoriel (je présume) ou bitmap, logiciels gratuits ou payants, avec quel plafond de prix, sur Mac, PC autre ?
"J'aimerais savoir quel sont les outils les plus fiables pour créer des illustrations pédagogiques (sciences et ingénierie)."
Ta question est trop vague, en tout cas pour moi : images 2D, images 3D, vectoriel (je présume) ou bitmap, logiciels gratuits ou payants, avec quel plafond de prix, sur Mac, PC autre ?
limipl a écrit :
... du père senteur_honrable.
Hé hou ! Je ne suis pas encore ici ni "père" ni "pé-père".
Mais yassinbean semble s'en être allé, semble-t-il construire sa belle pyramide hors d'Al-za ... Nous osons escompter qu'elle daigne contempler les siècles.
Modifié par senteur_honrable (05 Feb 2015 - 08:33)